|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
In the above example the current flows from the battery [1] through the depressed bi-directional A key [2] to the plugboard or "Steckerbrett" [3]. The current proceeds through the unused and therefore closed A socket [3] via the fixed entry wheel or "Eintrittwalze" [4] through the scrambled wirings of the three rotors or "Walzen" [5] to arrive at the reflector or "Umkehrwalze" [6]. The reflector returns the signal via a different path back through the rotors [5] and entry wheel [4] to continue to the plugboard's opened S socket [7]. The cable with two plugs or "Stecker" [8] send the signal to the D socket that passes the signal to letter switch D [9] to light-up light bulb D.
The plugboard sends and receives the signals to and from the fixed entry wheel, either directly or swapped with another letter by a cord with plugs. When no plug inserted, the two sides of that socket are connected to each other by its bridge (red bar). When a plug is inserted, the bridge is lifted, disconnects the two sides of the socket, and the signal is redirected through the plug cord. It's impossible to insert the plugs the wrong way because each plug has a thick and thin pin.
Note that depressing a key will first step the rotors and then the sent the current through the rotors and the light bulb. If the key is released the light bulb will no longer light up. Therefore, when no key is depressed, the rotor position you see in the little windows is the position of the previous encrypted letter!
Below the mechanical and electrical setup of the Enigma, viewed from the right. In this example the wiring with three letter key switches, three light bulbs and one plug cord. On the right the connections to the fixed entry wheel, the battery box (grey surface) and the power selector. In reality, the wires are grouped in bundles of 26 wires to plugboard, entry wheel and lamp panel.
|
|
|
|
|
|
|
|
Additional
rotors used by Kriegsmarine M3 and M4 only:
The special fourth rotors, also called Zusatzwalzen or Greek rotors. Used on the Kriegsmarine M4 with thin reflectors only:
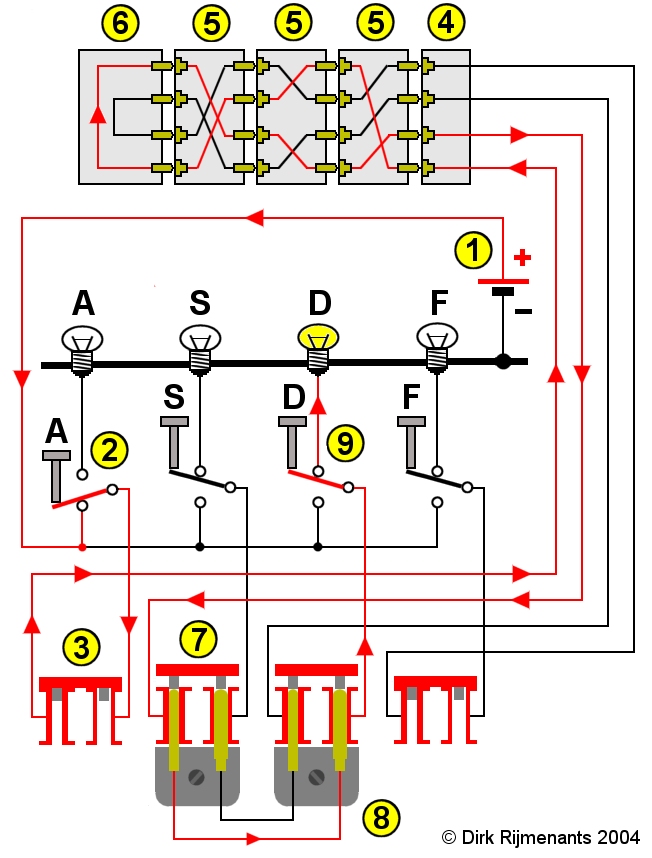
The reflector (Umkehrwalze or UKW in German) is a unique feature of the Enigma machine. On the normal rotors, each letter can be wired with any other letter. An 'A' could be wired to 'F', while the 'F' is wired to 'K'. In the reflector, the connections are made in loop pairs. In the case of the wide B reflector, the 'A' is wired to the 'Y' which means that the 'Y' is also wired to the 'A', resulting in a reciprocal encryption. The advantage of this design is that encryption and decryption are possible with the same machine setting and wiring. Unfortunately, a letter can never be encrypted into itself, a property that opened the door to cryptanalysis, making the job easier to the codebreakers. Default wide reflectors Wehrmacht and Luftwaffe:
Thin reflectors, Kriegsmarine M4 only:
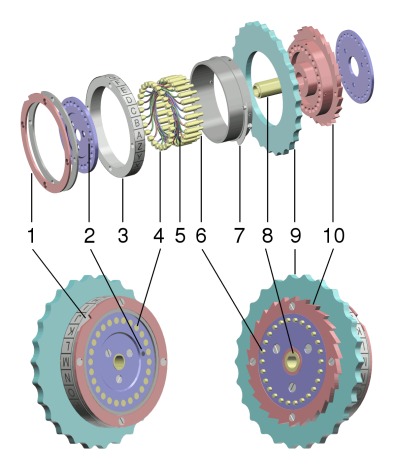
The wirings as described here, are for the rotors for Wehrmacht (Heer and Luftwaffe) and Kriegsmarine Enigma's only. The rotors for other versions of the Enigma machine had other internal wirings.
|
|||||
 The first example shows rotor I with
ring setting A-01 (pin or dot at A) and two
consecutive keystrokes of the letter A. Note that
the rotor was in the Z position before the first
keystroke and the rotor now has moved to the A
position.On the left you see rotor I in A position (A visible in the little window). The signal from the A key, arrives at the fixed entry wheel A position, enters the rotor at the A contact and exits at the E contact on the E position. On the right, the rotor has stepped to the B position. The signal again arrives at the A position, but now enters the rotor at the B contact and exits at the K contact. Since the complete rotor has stepped one position, the K contact is now in the J position and the signal therefore exits at the J position towards the next rotor. The 'Ringstellung' on the rotors is marked by a locking pin (Wehrmacht) or by a dot on the wiring core (Kriegsmarine). This marking shows the location of the first contact (A or 01) on the rotor core. Ring setting F or 06 thus will align the letter F or figure 06 on the outer ring with the first contact of the rotor, marked by the pin or dot. When changing the ring setting one position, the encryption is shifted one position. The rotor turnover point remains at the same letter, because the notch is located at the alphabet ring. The ring setting should not be confused with the rotor position, which is the letter on the alphabet ring, visible in the little window of the machine cover. |
|||||
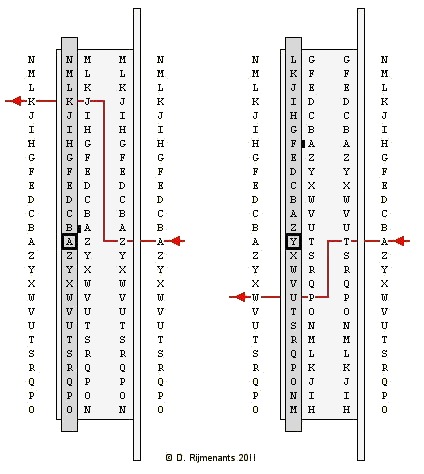 The next examples show the effect of
different ring settings.On the left, rotor I has a ring setting B-02 (pin or dot at B), the key is depressed and the rotor is in the A position (A visible in little window). The signal from the A key arrives at the fixed entry wheel A position. From the outside, the signal appears to enter the rotor at its A position, but in reality, it enters at the rotor's Z contact and exits at the J contact. Due to the ring setting, the wiring core is shifted one position and so do the exit contacts. Therefore, exit contact J is now in the K position and the signal exits at the K position towards the next rotor. This might be confusing, but that was the intention of the ring setting. On the right, we have the same rotor I with ring setting F-06 and the rotor in the Y position. The signal arrives at the entry wheel A position, enters the rotor at the T contact and exits at the P contact. However, the combination of the rotor position and its ring settings causes a shift of seven positions of the exit contacts. Therefore, exit contact P is now in the U position and the signal exits at the W position towards the next rotor. Note that the signal exits the rotor pack at the left. The reflector then returns the signal back through the rotors via another path to the right, again by a complex route, depending on rotor position and ring setting. There's an excellent on-line Java Enigma
simulation |
|||||
|
| Rotor | Notch | Window | next left rotor steps when rotor steps from/to |
I II III IV V VI VII VIII |
Y M D R H H + U |
Q E V J Z Z and M |
Q -> R E -> F V -> W J -> K Z -> A Z -> A and M -> N |
The three pawls on their axle,
resting on the pads. The pawl axle is
fixed to the stepping bar (silver L
shape). At the right of the pawls you can
see the fixed entry rotor. |
Gear type advance mechanism of the rare predecessor of the Enigma G. Notice the normal rotor contact placement instead of the later Enigma G rotors with special zigzag placed contacts. © D. Rijmenants |
Important note on the Stepping Sequence
KDO KDP, KDQ, KER, LFS, LFT, LFU…
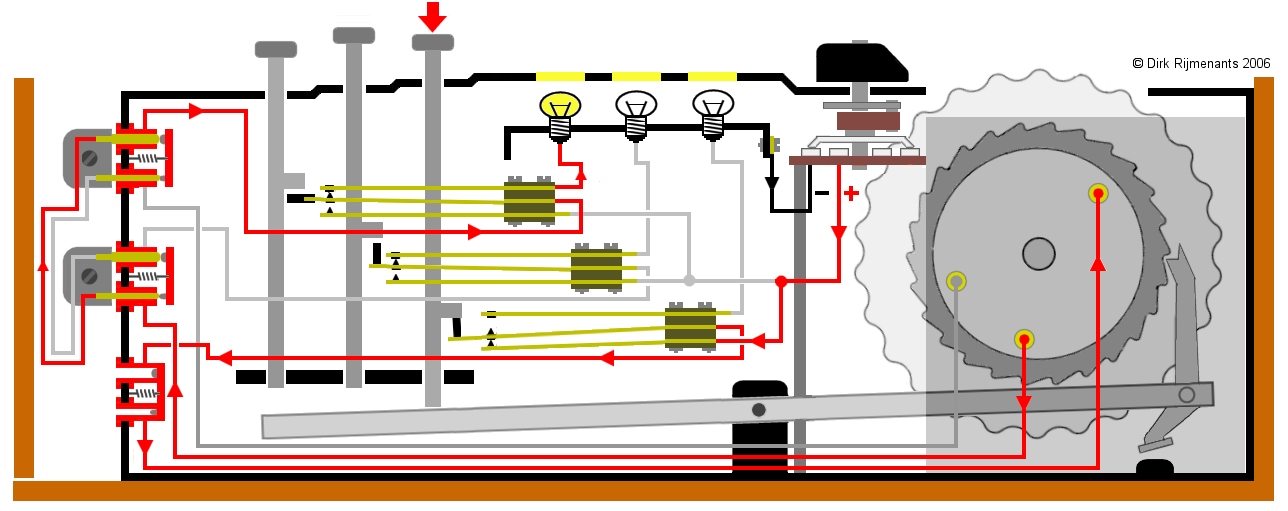
As you can observe, stepping from Q to R advances the middle rotor, and on the next step that middle rotor steps again, advancing the third rotor also. This is caused by the mechanical design of pawls and ratchets. There are three pawls that are all three activated on every key stroke. Each pawl is half positioned on the index ring (carrying a notch) of the rotor on its right, and half positioned above the 26 teeth of the rotor on its left (viewed from the point of the operator). A rotor’s ring prevents the pawl from pushing into the teeth of the next-left rotor. When a notch occurs in a ring, the pawl can drop into that notch and push into the teeth of the next-left rotor. Since the right-most pawl is not above an index ring it will continuously advance the right-most rotor.
Once the right-most rotor has stepped and the middle (spring-loaded) pawl can drop down in the right rotor's notch, it will engage the middle rotor's teeth, pushing the middle rotor one step. An identical event will take place when the middle rotor's notch enables the third pawl to drive the teeth of the left-most rotor. A rotor will not only advance if its teeth are catched, but also when a pawl pushes into its notch.
This situation creates a double-step of the middle rotor: the right rotor steps and the middle pawl takes the middle rotor one step further. If the middle rotor has moved by this step into its own notch position, then, on the next step, the left-most pawl catches the teeth of the left-most rotor, but the same pawl also pushes in the middle rotor's notch, moving it a second time in a row. Note that a double notched rotor in the middle position will also have two double steps.
The stepping mechanism, as explained above, is used on the Wehrmacht and Kriegsmarine Enigma. The four-rotor Kriegsmarine M4 is derived from the three rotor version without changing the rotor advance mechanism or adding a fourth pawl. Therefore the fourth rotor doesn't move and can only be adjusted manually. The Enigma-G, used by the Abwehr (German Intelligence) has a different mechanism. The Enigma-G has a rotating reflector and three rotors with multiple notches, rotated by a gear box.
The Plugboard 
In 1930, the plugboard
or Steckerbrett was introduced on the first
Wehrmacht Enigma version. The plugboard is
situated on the front of the machine. Without an
inserted plug, the current flows from the
switches, controlled by the keyboard, directly to
the entry rotor. Inserting a cable results in
swapping the two involved letters before
proceeding to the entry rotor. Each machine was
by default equipped with a set of 10 cables. The
plugboard was an important improvement of the
machines encryption strength.
Each letter has two jacks. Inserting a plug disconnects the upper jack, connected to the keyboard, and the lower jack, connected to the entry wheel. The other end of the cross-wired cable is inserted into another letter's jack, swapping the connections of the two letters. The current passes through the plugboard once on its way to the rotors and another time on its way to the light bulbs. |
|
|
|
|
Mathematical Security
, all possible
variations of wiring in each of the rotors and the
reflector was included. This results in an astronomical 3
x 10114. However, these misleading figures
represent all theoretically possible variations of the
machine.
Unfortunately for the Germans, the Allied codebreakers knew the machine, the rotors and the internal wiring of these rotors. Therefore, they only had to take in account the actual possible ways you could set the machine, the actual key settings or key space. This is what we call the practical security, which is far less than the theoretical security in the case of Enigma. For the German cryptologists, a single rotor could be wired in 4 x 1026 different ways. Combining three rotors and a reflector quickly gives you astronomical figures.
For the Allied codebreakers, who knew
the wring of the rotors, there were only 26 different
variations for a single rotor, that is, the 26 positions
it could have in the machine. They didn't have to search
through the immense number of possible wirings. The
German cryptologists made a critical mistake by ignoring
Auguste Kerckhoff's law that the security of a device may
never depend on the secrecy of the system (i.e. rotor
wiring, design), which will be compromised sooner or
later anyhow, but only on the secrecy of the key (i.e.
rotor selection and plugboard). In the interesting R.A. Ratcliff paper for Cryptologia
you can read how dangerous it is to rely on theoretical
security.
Let us look at all the things we can actually set in the machine and are unknown to the codebreaker. In our example, we take the three-rotor Wehrmacht Enigma with default B reflector and selection out of 5 rotors. We use 10 plug cables on the plugboard, the default number of cables, issued with the machine (don't ask me why they didn't provide 11 cables, which gave far more possible combinations)
To select 3 rotors out of a possible 5, there are 60 combinations (5 x 4 x 3). Each rotor, in other words its internal wiring, can be set in any of 26 positions. Therefore, with 3 rotors there are 17,576 different rotor positions (26 x 26 x 26). The ring on each rotor holds the rotor labelling (which doesn't matter here) and a notch that affects the stepping of the next-left rotor. Each ring can be set in any of 26 positions. As there is no rotor to the left of the third (most-left) rotor, only the rings of the most-right and middle rotor affect the calculation. This gives 676 ring combinations (26 x 26).
The plugboard provides the largest chunk of possible different settings. For the first cable, one side can have any of the 26 positions and its other side any of the 25 remaining positions. However, since a combination and its reverse are identical (A-B is the same as B-A) we have to ignore all doubles in all possible combinations for one cable, giving (26 x 25) / (1! x 21) or 325 unique ways to set one cable. For two cables, we have (26 x 25) for the first cable and, since two sockets are already used, (24 x 23) for the second cable. We now have to take in account the doubles for two cables, giving (26 x 25 x 24 x 23) / (2! x 22) = 44,850 unique ways to set two cables. For three cables we have (26 x 25 x 24 x 23 x 22 x 21) / (3! x 23) = 3,453,450 combinations, and so on. Thus, with the default 10 cables we have 150,738,274,937,250 different combinations. The formula, with n as the number of cables, is 26! / (26 - 2n)! · n! · 2n
In total, this gives: 60 x 17,576 x 676 x 150,738,274,937,250 = 107,458,687,327,250,619,360,000 or 1.07 x 1023
So, in real life, the Wehrmacht Enigma machine could be set in 1.07 x 1023 different ways, which is comparable with a 77 bit key.
There are some comments we should add to this number. In reality, the maximum period of the rotors - the number of steps before the machine repeats itself - is slightly less than 17,576. This is caused by the double-step feature of the stepping mechanism. The actual period depends on the type of rotor. The three double-notched Naval rotors will have an even smaller period than the Wehrmacht rotors as they produce more double steps of the middle rotor. The maximum period however is no part of the variables that can be set and therefore do not influence the key space.
The Wehrmacht machine could be equipped with either the B or C reflector. In general, radio nets always used the same reflector, as the use of different reflectors created logistical, procedural and practical problems. If nonetheless taken in account, the choice between B and C reflector would only double the key space.
The adding of a fourth rotor for the Naval Enigma M4 to improve its security was a nice but useless addition. The non-moving fourth rotor complicated the machine only by a factor 26 and, together with the thin reflector, could be considered as a settable reflector with 26 positions, of which the Allies quickly found the wiring (after 10 months of panic). The introduction of 8 naval rotors on the Kriegsmarine M3 and later on the four-rotor M4 was a far better approach. They increased the rotor combinations from 60 to 336, and brought in additional complexity with 3 multiple notched naval rotors VI VII and VIII.
Let us now calculate the practical key size of the four-rotor Kriegsmarine Enigma M4. This machine uses 3 normal rotors, selected from a set of 8 (of which three with double notches). This gives 336 rotor combinations (8 x 7 x 6). The M4 also has a special fourth rotor called Beta or Gamma (without a ring), which gives us 2 choices. These are not compatible with the other rotors and are only suitable as fourth (most left) rotor. The 4 rotors can be set in any of 456,976 positions (26 x 26 x 26 x 26). The M4 had a smaller B or C reflector, to enable the placement of the fourth rotor. We don't include the choice of reflector as it was generally never changed. Again, only two rings were involved, as the third rotor didn't step the never moving fourth rotor. The M4 was also issued with 10 plug cables.
In total, this gives: 336 x 2 x 456,976 x 676 x 150,738,274,937,250 = 31,291,969,749,695,380,357,632,000 or 3.1 x 1025, comparable with a 84 bit key.
This is about 291 times stronger than the Wehrmacht machine. This is due to the increased choice of rotors (already available on the M3 before the war) and the possible initial positions for 4 rotors instead of 3. However, although the fourth rotor did increase the key size, it failed to add to the complexity of the encryption itself, since it couldn't move during the enciphering process.
A better solution would have been to completely re-wire some of the rotors on a regular basis. A single variable rotor wiring would multiply the key space with no less than 4 x 1026, which is far more than a settable reflector with its 7.8 x 1012 possible variations. A single practical, daily changed, rewireable rotor, which has 4 x 1026 possible settings, would have been much more effective than the overestimated daily not-moving plugboard setting with only 2 x 1014 variations (the plugboard was always in pairs). The use of such rotor, for instance in conjunction with a thin M4-like reflector and two out of four normal rotors, would be a true disaster for the codebreakers.
However, introducing rewireable rotors during wartime would be cumbersome and present a logistical and financial nightmare, just as the rewireable D reflector proved to be. Too little too late. The D reflector did scare the codebreakers initially, until they realized that the D reflector was used simultaneously with the default reflectors in the same radio nets, due to practical considerations. This dual use made it possible to break it even by hand. More about the D reflector and other attempts on the Enigma history page.
Any crypto-expert would also discard the 17,576 ring combinations. Even with completely wrong ring settings, you will initially start with a correct plain text. As soon as you get garbled text, you adjust the ring of the most-right rotor (a 1/26 chance you're right) and if you're lucky you have no more trouble for the next 676 characters. If less lucky, you had to adjust the ring of the middle rotor after 26 letters. All done on-the-fly. Unfortunately for the Germans, the ingenious Turing Bombe design, with mirrored identical rotor packs, avoided the need to search through the immense number of plugboard settings, taking a factor 2 x 1014 shortcut on the linking of their cribs (known piece of plain and ciphertext) to a given rotor setting.
Breaking the Enigma traffic was nonetheless an enormous challenge with a key setting that was extraordinary in the electro-mechanical era of those days. An exhaustive search on 1.07 x 1023 settings was impossible in the 1940s and its comparable 77 bit key is even huge for today's computer standards. To give you an idea of the size of that number, with 1.07 x 1023 sheets of paper (0.0039 inch each) you can build roughly 70,000,000 stacks of paper, each of them reaching from the Earth to the Sun. Also, 1.07 x 1023 inches equals 288,500 light-year. A pretty big number!
The Germans were correct in assuming
that the Enigma was theoretically unbreakable. However,
codebreaking is more than keys sizes and numbers,
theoretical security and searching for the right
combination, and the allies proved them wrong. More on Enigma and the
U-boat war.
More on Enigma on this Website
- Enigma Menu directing you to the various Enigma pages.
- References
More on the Technical Details of the Enigma (off-site, opens in new tab)
- Enigma 3D video created by Jared Owen Animation with inside view of the electrical and mechanical processes.
© Dirk Rijmenants 2004. Last changes: 24
August 2022
| Home Menu History Procedures Technical details Enigma Simulator |